本文为第一系列的原创文章之二, 目的在于总结 “Simulation” -Sheldon M.Ross 一书中出现的模拟随机变量的方法.
泊松分布与二项分布
在本站先前的文章 Gamma 函数与 Beta/Dirichlet 分布中提到过二项分布, 其本质是离散形式的 beta 分布, 二项分布的表达式为:
\begin{align*} P(x=k) &= C_n^kp^i(1-p)^{(n-k)} \\\ &=\frac{n!}{k!(n-k)!}p^i(1-p)^{(n-k)} \end{align*}
当我们尝试产生一个服从二项分布的随机数时, 我们一般通过迭代关系求出 \(P(x=i)\) , 然后产生一个 \((0,1)\) 的均匀分布, 将均匀分布映射到通过迭代关系式划分出的二项分布的区间上.
(不直接计算 \(P(x=i)\) , 因为会涉及到 \(3n\) 个阶乘运算, 也不采用 \(n\) 次独立重复试验的方法, 因为需要产生 \(n\) 个随机数.)
很显而易见的, 对于二项分布 \(B(n,p)\) 我们有:
\begin{align*}\frac{P(x=i+1)}{P(x=i)}&=\frac{n-i}{i+1}\frac{p}{1-p} \\\ P(x=0)&=(1-p)^n \end{align*}
记 \(p_i = P(x=i)\) , 令 \(x_i = \sum_{k=0}^{i}p_k\) , 并令 \( x_{-1} = 0\), 这样可以求出所有 \(x_i\) 的值, 并且这些值将 \((0,1)\) 划分为 \(n + 1\) 个小区间.
接下来生成 \(U \sim Uniform(0,1)\) , 若 \(U\) 落在区间 \([x_{i-1}, \ x_i)\) 内, 即若有:
\[x_{i-1} \leq U < x_i\]
那么生成的二项分布的变量即为 \(x_i\). (\(0\leq i \leq n\))
对于 Poisson 分布, 类似的思路我们可以得到:
\[ p_i = P(x=i)=e^{-\lambda}\frac{\lambda^i}{i!}, \quad\quad i=0,1,2,…\\ \frac{p_{i+1}}{p_i}=\frac{\lambda}{i+1}\]
然而, 很明显, Poisson 分布有无数项, 不可能使用上述的方法进行迭代. 依据柯西收敛定理可以知道, \(p_i\) 一定会收敛到某特定截断误差以内, 所以我们可以根据要求的近似程度对尾部做一个截断, 即找到一个足够大的 \(N\) , 并认为:
\[P(x\geq N) \approx P(x=N)\]
在这里不加证明的给出, 平均搜索的次数为 \(1 + E[|X-\lambda|]\) , 其中 \(X \sim N(\lambda, \lambda)\), 即平均搜索的次数大概为 \(1 + 0.798\sqrt{\lambda}\).
值得一提的是, 对于二项分布 \(B(n,p)\) , 令\(\lambda=np\), 当 \(n \rightarrow \infty\) :
\begin{align*} P(x=k)&=\frac{n!}{k!(n-k)!}p^i(1-p)^{(n-k)}\\\ &=\frac{n!}{k!(n-k)!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k}\\\ &=\frac{n(n-1)…(n-k+1)}{n^k}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k}\\\ &=e^{-\lambda}\frac{\lambda^k}{k!} \end{align*}
运用的极限等式有
\begin{equation}\lim_{n \rightarrow \infty}(1-\frac{\lambda}{n})^{n-k} = e^{-\lambda};\\\ \lim_{n \rightarrow \infty}\frac{n(n-1)(n-2)…(n-k+1)}{n^i}=1 \end{equation}
也就是说, 当 \(n\) 很大时, 可以认为二项分布近似为泊松分布.
Matlab 模拟
我们针对二项分布进行了 Matlab 代码的模拟
function k = binomial_random_variable(n,p,N)
k = zeros(1,N);
for i = 1:N
c = p/(1-p);
pk=(1-p).^n;
sum = pk;
random = rand(1,1);
while(sum < random)
pk = pk * c * (n - k(i)) / (k(i) + 1);
sum = sum + pk;
%%可以理解为概率在[0,1]上增长, 当增长到均匀分布U产生的位置, 增长次数可以认为U落在的区间数, 即生成的随机变量k(i)
k(i) = k(i) + 1;
end
end
end
模拟了 \(N\) 个服从 \(B(n,p)\) 的独立同分布的随机变量作为返回值. 我们接下来执行:
clear;
n=40;
p=0.5;
N=10000;
k= binomial_random_variable(n,p,N);
subplot(2,1,1);
hist(k,1:n);
axis([0,n,0,N*0.15]);
out=hist(k, 1:n);
hold on;
out=out./N;
subplot(2,1,2);
stem(1:n,out,'filled');
可以绘出图像:
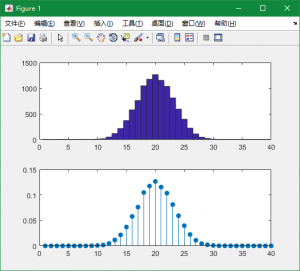
比较符合我们对于二项分布的预期.
5 thoughts on “统计模拟(二)——泊松分布与二项分布模拟”