本文为第一系列的原创文章之三, 目的在于总结“Simulation” -Sheldon M.Ross一书中出现的模拟随机变量的方法.
Acceptance-Rejection
在介绍正态分布的模拟前先介绍一种方法, 叫做 Acceptance-Rejection Technique. 这种方法一般用于生成比例形式的随机变量(往往用比例形式更好模拟的情况下.)
对于离散型的随机变量, 假设我们想要模拟的变量为 \(q_i\) , 已知可以模拟的变量为 \(p_i\) ,大致的做法如下:
1.选取一个常数 \(c\) 需要满足: 对于所有的 \(i\), 有 \(c \geq \large\frac{q_i}{p_i}\) ;
2.模拟出变量 \(Y\), 满足的离散分布为 \(p_i\) ;
3.生成一个服从 \((0, 1)\) 均匀分布的变量 \(U\) ;
4.如果 \(U < \large\frac{q_y}{cp_y} \), 接受, 使 \(X=Y\) 并停止, 否则执行2.
可以证明
\[P(Y=i, 第k次循环被接受) = p_i \frac{q_i}{cp_i}(1-\frac{q_i}{cp_i})^{k-1}, \quad\quad k=1,2,…,n, … \]
\begin{align*} P(X=i)&=\sum_{k=1}^{+\infty} P(Y=i, 第k次循环被接受)\\\ &= p_i \frac{q_i}{cp_i}\sum_{k=1}^{+\infty}(1-\frac{q_i}{cp_i})^{k-1}\\\ &=p_i \cdot \frac{q_i}{cp_i} \cdot \frac{p_i}{cp_i}\\\ &=p_i \end{align*}
类似地, 我们可以推广到连续型随机变量上, 步骤如下:
-
生成密度函数为 \(g\) 的变量 \(Y\) ;
-
产生一个服从 \((0,1)\) 随机分布的变量 \(U\) ;
-
如果 \(U \leq \dfrac{f(Y)}{cg(Y)}\) , 令 \(X=Y\) , 否则继续执行1.
Uniform Distribution Simulation
接下来, 我们考虑模拟生成标准正态分布的过程, 标准正态分布的表达式为:
\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \quad\quad -\infty<x<+\infty\]
为了将指数部分分离出来, 可以构造一个指数分布的分布函数:
\[g(x)=e^{-x}\quad\quad 0<x<+\infty\]
注意到此处指数分布的区间与正态分布不同, 为了使 Acceptance-Rejection 生效 , 我们可以令 \(\hat{f}(x) = f(|x|)\), 得到在区间 \(0<x<\infty\) 的分布, 最后对模拟结果随机取 \(+X\) 或者 \(-X\) 即可. 于是我们可以得到需要的常数 \(c\) 满足:
\[ c=max(\frac{\hat{f}(x)}{g(x)})=max(\frac{2}{\sqrt{\pi}}e^{x-\frac{x-x^2}{2}})\\ =\frac{2f(1)}{g(1)}=\sqrt{\frac{2e}{\pi}} \]
于是我们有:
\[\frac{\hat{f}(x)}{cg(x)}=e^{-\frac{(x-1)^2}{2}}\]
另外, 对于指数分布的模拟, 我们只需生成一个标准的均匀分布, 然后取自然对数再取相反数, 便可得到我们所需要的服从 \(g(x)\) 的指数分布. (证明略). 那么我们便可得到生成正态分布的模拟步骤:
1.生成均匀分布 \(U_1\) , 令 \(Y=-ln(U_1)\);
2.生成均匀分布 \(U_2\) , 如果 \(U_2\leq e^{-\dfrac{(y-1)^2}{2}}\) , 执行3, 否则执行1;
3.生成均匀分布 \(U_3\) , 如果 \(U_3 > 0.5\), 令 \(X=-Y\) , 否则令 \(X=Y\);
Matlab Simulation
根据其实现, 写出的Matlab代码进行验证:
clear;
N = 10000000;
n = 1000000;
x=zeros(1,n);
u1=rand(1,N);
u2=rand(1,N);
u3=rand(1,N);
y=-log(u1);
i = 1;
j = 1;
while i < n
if u2(j) < exp(-((y(j) - 1).^2)/2)
if u3(i) > 0.5
x(i) = -y(j);
i = i + 1;
else
x(i) = y(j);
i = i + 1;
end
end
j = j + 1;
end
subplot(2,1,1);
hist(x, -8:0.1:8);
hold on;
[field, out] = hist(x, -8:0.1:8);
field = field./n;
subplot(2,1,2);
bar(out, field);
mu = sum(X) ./ n ;
sigma = sum((X - mu).^2 ./ n);
绘制出的图像如下, 下方的子图为其模拟的分布函数:
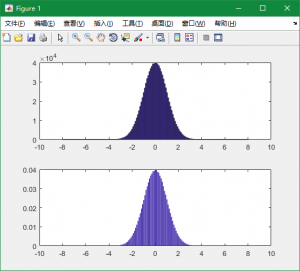
得到验证的 \(\sigma^2\) 与 \(\mu\) 的值约为 \(0.99991271\) 与 \(-0.00055450\) .
Polar Method
除了使用接受-拒绝方法之外, 也可以使用二维正态分布的生成方法, 生成一对极坐标的变量, 这一对极坐标经过一个变换, 可以变换成一对二维正态分布的随机变量, 这一对变量中的任意一个都是一个正态分布. 这个变换方法, 我们称之为 Box-Muller 变换.
假设 \(X\) 与 \(Y\) 是相互独立的正态分布, 用 \(r\) 与 \(\theta\) 表示 \((X, Y)\) 对应的极坐标, 有:
\begin{equation}\begin{cases}r^2 = X^2 + Y^2\\\ \theta = arctan \frac{Y}{X} \end{cases}\end{equation}
由于 \(X\) 与 \(Y\) 相互独立, 二者的联合概率密度有
\begin{equation} f_{X,Y}(x,y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}} \end{equation}
我们令 \(R=r^2\) 那么对 \(R\) 和 \(\theta\) 进行变换, 有:
\begin{equation} f_{R,\theta}(R, \theta)= \frac{1}{det(\mathcal{J})}\frac{1}{2\pi}e^{-\frac{R}{2}} \end{equation}
其中, \(\mathcal{J}\) 为该变换的雅各比行矩阵:
\begin{align*} det(\mathcal{J}) &=\begin{vmatrix}\dfrac{\partial R}{\partial x} & \dfrac{\partial R}{\partial y} \\\ \dfrac{\partial \theta}{\partial x} & \dfrac{\partial \theta}{\partial y}\end{vmatrix}\\\ &=\begin{vmatrix}2x & 2y \\\ -\dfrac{y}{x^2+y^2} & \dfrac{x}{x^2+y^2}\end{vmatrix}\\\ &=2 \end{align*}
最后, 我们模拟生成一个指数分布与均匀分布, 便可利用极坐标的转换, 转换成二维的正态分布.
步骤如下:
1.生成标准的均匀分布的随机变量 \(U_1\) 与 \(U_2\) .
2.令
\begin{align*} r&=\sqrt{-2lnU_1}\\\ \theta&=2\pi U_2\\\ \end{align*}
3.令
\begin{align*} X&=rcos\theta=\sqrt{-2lnU_1}cos(2\pi U_2)\\\ Y&=rsin\theta=\sqrt{-2lnU_1}sin(2\pi U_2) \end{align*}
\(X, Y\) 便是我们需要的二维正态分布.
Improved Polar Method
事实上, 生成随机角度时需要计算三角函数, 我们知道, 计算机计算三角函数是利用泰勒展开式进行逼近, 当运算任务比较重时, 会成为一个运算的短板.
在实际的使用中, Box-Muller 变换可以使用以下方法模拟三角函数.
令
\[ Z_1 = 2U_1 – 1 \\ Z_2 = 2U_2 – 1\]
我们去掉 \(Z_1^2 + Z_2^2 \geq 1\) 的部分, 那么对于点 \([Z_1, Z_2]\) 是“均匀”落在一个单位圆内.
此处的均匀的意思是指, 对于单位圆的极坐标 \(r, \theta\) , 其中 \(r \sim Uniform(0,1)\) , \( \theta \sim Uniform(0,2\pi)\). (原因是直角坐标到极坐标的雅各比矩阵是常数, 证明略.)
所以我们有:
\begin{align*} &sin\theta = \frac{Z_1}{r}\\\ &cos\theta = \frac{Z_2}{r}\\\ &r=\sqrt{Z_1^2+Z_2^2} \end{align*}
之前令 \(R=r^2\) , 那么带入到先前的表达式中:
\begin{align*} X&=Z_1\sqrt{\frac{-2lnR}{R}}\\\ Y&=Z_2\sqrt{\frac{-2lnR}{R}}\end{align*}
这样修改后的 Box Muller 变换进行模拟的过程如下:
1.生成标准的均匀分布的随机变量 \(U_1\) 与 \(U_2\) .
2.令
\begin{align*} &Z_1 = 2U_1 – 1 \\\ &Z_2 = 2U_2 – 1 \\\ &R = Z_1^2 + Z_2^2\\\ \end{align*}
3.如果 \(R \geq 1\) , 则返回1 , 否则执行4
4.令
\begin{align*} X&=Z_1\sqrt{\frac{-2lnR}{R}}\\\ Y&=Z_2\sqrt{\frac{-2lnR}{R}}\\\ \end{align*}
这个算法一共需要产生 \(2\times\dfrac{4}{\pi} \approx 2.546\) 次随机数, 一次对数运算, 一次除法运算, 一次开方运算. 而不再需要三角函数运算, 这样计算的 \(X\) 与 \(Y\) 拥有更小的时间复杂度.
参考代码
由于 matlab 独特的方便矩阵运算的特性, 循环运算在 matlab 中并没有优势. 此处贴出代码仅供参考. (时间复杂度的估计并不理想.)
原方法:
%% file name : BoxMuller1
clear;
N = 100000000;
U1 = rand(1,N);
U2 = rand(1,N);
tic;
R = sqrt(-2*log(U1));
c = cos(2 * pi * U2);
s = sin(2 * pi * U2);
X = R.*c;
Y = R.*s;
clear c s U1 U2 R;
toc;
subplot(2,1,1);
hist(X, -8:0.1:8);
hold on;
[field, out] = hist(X, -8:0.1:8);
field = field./N;
subplot(2,1,2);
bar(out, field);
mu = sum(X) ./ N;
sigma = sum((X - mu).^2 ./ N);
改进方法:
%%file name: BoxMuller2
clear;
n = 130000000;
N = 100000000;
Z1 = 2 * rand(1,n) - 1;
Z2 = 2 * rand(1,n) - 1;
R = Z1.^2 + Z2.^2;
map = find(R>1);
Z1(map) = [];
Z2(map) = [];
R(map) = [];
tic
Z1 = Z1(1:N);
Z2 = Z2(1:N);
R = R(1:N);
S = sqrt(-2 * log(R) ./ R);
X = S .* Z1;
Y = S .* Z2;
clear Z1 Z2 S R;
toc;
subplot(2,1,1);
hist(X, -8:0.1:8);
hold on;
[field, out] = hist(X, -8:0.1:8);
field = field./N;
subplot(2,1,2);
bar(out, field);
mu = sum(X) ./ N;
sigma = sum((X - mu).^2 ./ N);