问题背景
本问题来源于实际问题,社交平台设计上为了保证回复帖的并发一致性,需要在回复帖前获取楼层的分布式锁,获取分布式锁的可以有资格修改存在Redis中的楼层数。目前逻辑是,如果竞争分布式锁失败,那么会直接报错,用户感知发帖失败。现在怀疑该设计会使得错误率随着QPS的提升有显著提升。本文从该问题出发,使用泊松分布与指数分布作为基本模型,探讨系统性能随容量变化的趋势。
问题描述与模型建立
问题描述如下。现有一社交平台,用户会有以下操作:
1. 发主题帖
2. 回复主题帖
存在如下碰撞可能,某一主题帖如果没有任何回复内容,在时间\( t_q\)内被至少一个用户回复,会发生碰撞。现已知每日主题帖的数量为\( Pst\),每日回复主题帖的数量为\( Rpst\),求每日发生碰撞次数的分布,并且探讨随着平台的使用量增大,碰撞概率发生变化的趋势。
用户在社交平台上针对某一主题帖进行回帖,可以看作服从泊松分布。有关泊松分布,可以参考本站先前的博客统计模拟(二)——泊松分布与二项分布模拟与统计模拟(六)——保险模型有关泊松分布的叙述。
用通俗的语言解释泊松分布,如现在已知每家海底捞在高峰时段平均每小时招待150名客人,求高峰时期招待用户数量的分布。
\[
P(X(t)=k)=e^{-\lambda t}\dfrac{(\lambda t)^i}{k!}
\]
其中 \( \lambda\) 为单位时间内的事件发生概率,为了求2.5小时内招待350-400名客人的概率,可以将代入参数:
\[
\sum_{k=350}^{400} P(X(k)) =\sum_{k=400}^{500} \dfrac{(150 \times 2.5)^k e^{(-150 \times 2.5)}}{k!} \approx 0.8122
\]
泊松分布与指数分布有着密不可分的关系,从当前时刻开始计算,时间 t 内事件发生的概率服从指数分布。(等价于时间 t 内事件发生次数不为0)
\[
P(X < t) = 1 – e^{-\lambda t}
\]
在本问题中,每个主题帖每秒钟平均的回复数为\( \lambda = Rpst/86400/Pst\)。假设当前存在一个主题帖,在24h内无人回复会沉帖。那么该主题帖的状态的转移状态为:
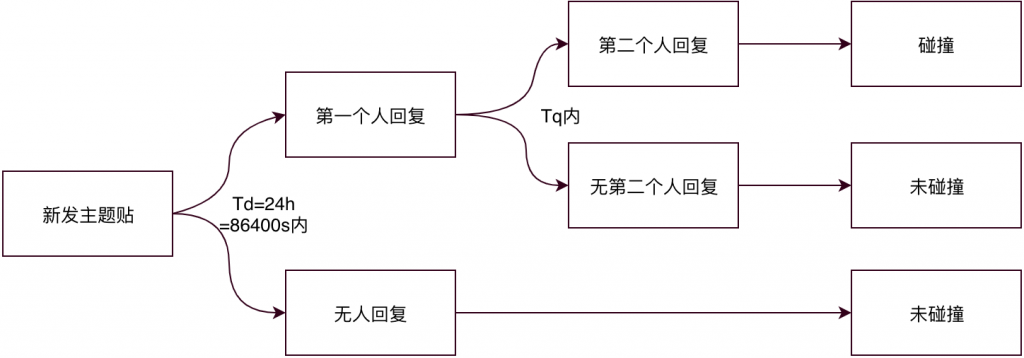
回复的时间间隔服从指数分布
\begin{align*}
P(x\le t_d)= 1 – e^{-\lambda_1 t_d}\\
P(x\le t_q)= 1 – e^{-\lambda_1 t_q}
\end{align*}
对于某个特定帖子发生碰撞的概率
\[
P(conflict) = P(x\le t_d) P(x\le t_q)
\]
记\( P(confilct)\)为\( \beta\)
当前每天的主题帖的分布为
\[
P(X = n)=\dfrac{(\lambda_2 t_d)^n e^{-\lambda_2 t_d}}{n!}
\]
不同主题帖之间的回帖我们认为是独立事件,所以可以将一天之内的分布碰撞看作独立同分布的事件,于是一天之内的碰撞次数的分布为
\[
P(x=m)=C_n^m(1-\beta)^{n-m}\beta^m
\]
问题的数值推演
首先考虑 \( \beta\) 中 \( \lambda_1\) 的取值,\( \lambda_1\) 描述了单位时间(秒)之内新发主题帖平均的回复数量,\( \lambda_1 t_d\) 为一天之内平均每条主题帖的回复数 \( Q\),数字量级为\( 10^1\),可以近似得到
\[
P(x\le t_d) \approx 1
\]
\( \lambda_1 t_q\) 实际取值为\( \frac{t_q}{t_d}Q \) ,数字量级为\( 10^{-6}\),即对于单一帖子而言,碰撞概率大约在百万分之一。该数量级下直接对 \( P(x \le t_q)\) 进行一阶泰勒展开,可以得到:
\[
P(x\le t_q)= 1 – e^{-\lambda_1 t_q} = \lambda_1 t_q
\]
不妨代入假设数字进行验证。令每日主题帖数量为2500,每日回复帖为1000计算得到:
\[
P(x \le t_d)= 1 – e^{- 10000/2500} \approx 0.98 \approx 1
\]
令 \( t_q = 0.025s\) 计算得到
\[
P(x \le t_q) = 1 – e^{-10000\div 2500\div 86400\times 0.025} \approx 1.16 \times 10^{-6}
\]
先不考虑每天主题帖的 \( n\) 分布变化,考虑现在新发主题帖的回复为之前的 \( k\) 倍,即 \( \lambda’_1 = k \lambda_1\),单一帖子的碰撞概率:
\begin{align*}
P'(x\le t_q) &= k \lambda_1 t_q \\
P'(x\le t_d) &\approx 1
\end{align*}
于是有
\[
\beta’ = k\beta
\]
一天之内碰撞的分布:
\[
P'(x=m)=C_n^m(1-\beta’)^{n-m}\beta’^m
\]
计算现在的分布与之前的分布的变化倍数\( K_1\):
\begin{align*}
K_1&=\lim_{\beta\rightarrow 0}\dfrac{P'(x=m)}{P'(x=m)}\\
&=\lim_{\beta\rightarrow 0}\dfrac{C_n^m(1-\beta’)^{n-m}\beta’^m}{C_n^m(1-\beta)^{n-m}\beta^m}\\
&=\lim_{\beta\rightarrow 0}(1+\dfrac{\beta-\beta’}{1-\beta})^{n-m}(\dfrac{\beta’}{\beta})^m\\
&=\lim_{\beta\rightarrow 0}e^{-(k-1)\beta(n-m)}k^m\\
&=k^m
\end{align*}
考虑发生至少一次碰撞的概率
\[
P(x\geqslant 1)=1-(1-\beta)^{n-m}
\]
计算至少一次碰撞的概率变化倍数 \( K_2\)
\begin{align*}
K_2&=\lim_{\beta\rightarrow 0}\dfrac{P'(x\geqslant 1)}{P(x\geqslant 1)}\\
&=\lim_{\beta\rightarrow 0}\dfrac{1-(1-\beta’)^{n-m}}{1-(1-\beta)^{n-m}}\\
&=\lim_{\beta\rightarrow 0}\dfrac{1-(1-\beta’)^{n-m}}{1-(1-\beta)^{n-m}}\\
&=k
\end{align*}
(竟然都把 \(n \)都消掉了)
结果
虽然很不甘心,但是推算结果的确与猜测不符。
附录
为了计算
\[
\sum_{k=350}^{400} \dfrac{(150 \times 2.5)^k e^{(-150 \times 2.5)}}{k!}
\]
主要有以下多个考虑
1. \( 375^k \) 太大
2. \( k! \) 太大
3. \( e^{375} \) 太大
主要就是将以上三个数拆分成
1: \( k\)次乘除法,2: \( k\)次乘除法,3: \( 375\)次乘除法 代码如下
double sum = 0;
for(int k = 350; k <= 400; k ++){
int counter = 375;
double temp = 1d;
for(int j = k; j > 0; j --){
temp *= 375d / j;
while(counter > 0 && temp > 10){
temp /= Math.E;
counter --;
}
}
while(counter > 0){
temp /= Math.E;
counter --;
}
sum += temp;
}
System.out.println(sum);