Redis 支持基于 HyperLogLog 的基数计数统计,其算法思想和前两篇提到的 Linear Counting 和 LogLog Counting 的算法类似,本篇主要分析其源码——github:antirez/redis/src/hyperloglog.c 中的代码
Header
Header 总共有 16 个字节,分别为
HYLL E N/U Cardin
如下图所示:

HYLL 是 4 个魔法字节,为”HYLL”
E 为 1 个字节表示Dense/Sparse
N/U 为未来留下的空字节,共 3 个字节
Cardin 为缓存区,8 个字节
代码实现如下:
struct hllhdr {
char magic[4]; /* "HYLL" */
uint8_t encoding; /* HLL_DENSE or HLL_SPARSE. */
uint8_t notused[3]; /* Reserved for future use, must be zero. */
uint8_t card[8]; /* Cached cardinality, little endian. */
uint8_t registers[]; /* Data bytes. */
};
所以 HyperLogLog 整体的内部结构就是 hllhdr 以及 16384 个桶的计数值位图。在 Redis 的内部结构表现就是一个字符串位图。可以把 HyperLogLog 对象完全当成普通的字符串来进行处理。其字符头为 “HYLL\x00” 或者 “HYLL\x01″,满足这种条件的字符可以使用 HyperLogLog 指令。
接下来会主要介绍 Dense/Sparse 与缓存区的特性
Sparse
稀疏存储主要应用于多数的基数计数值为 0 的状况,在这种情况下对计数结果进行压缩,可以节省空间。稀疏存储情景下,Redis 使用了 3 个操作码表示不一样的计数结果。
ZERO 操作码的形式为 “00xxxxxx”,后面的 6 bits 表示后面是 xxxxxx + 1 个连续的 0
XZERO 操作码的形式为 “01xxxxxx yyyyyyyy”, 6 bits 的 “xxxxxx” 被称为 Most Significent Bits MSB,8 bits 的 “yyyyyyyy” 被称为 Least Significent Bits。14 个比特表示最多 2^14 = 16,384 个零值计数器
VAL 操作码的形式为 “1vvvvvxx”, 5 bits 的 “vvvvv” 表示的是重复的计数值, “xx” 表示重复计数值的桶的数量,即连续 (xx + 1) 个桶的计数值都是 (vvvvv+1)。能表示的计数值最大重复为 4 次, 计数值最大表示为 32,超过 32 将从 Sparse 转换到 Dense。
稀疏存储的例子如下图所示:
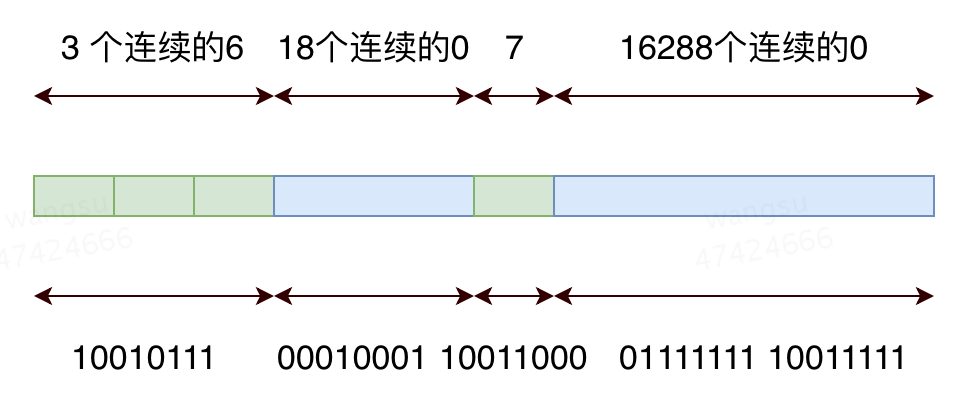
除了 VAL 操作码超过 32,稀疏存储的占用的总字节超过 3000 字节也会发生由 Sparse 到 Dense 的转换,这个阈值为 hll_sparse_max_bytes
Dense
当从稀疏存储转化为密集存储时,Redis 采用连续的 16384 个 6bits 字符串组成字符串,如下图所示:
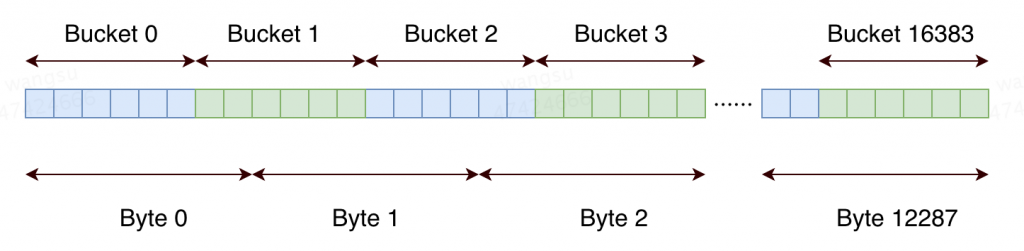
需要特殊注意的是,每个字节内存放的比特和一般字节内的左高右低不同,在连续的Bucekt 中字节位数相反,左低右高。
所以其比特级别的数据结果表示为:
|1100 0000|2222 1111|3333 3322|5544 4444|6655 5555|7777 6666|···
数字表示不同的桶的编号,例如第一个比特的 1100 0000 为第 1 个 bucket 的前 2 个 bits 与第 0 个 bucket 的 6 个 bits
相对于上图,需要将同一个字节中不同 bucket 的比特交换高低的位置。
当需要得到某个 pos 位置的桶的值时,需要先得到字节间偏移量:
bx = 6 * pos / 8
然后得到字节内的偏移量
by = 6 * pos % 8
将 bx 字节右移 by 个比特,将 b(x+1) 左移 8 – by 个比特,并进行按位或。
最后与 001111 按位将高 2 位舍弃得到最后的结果。
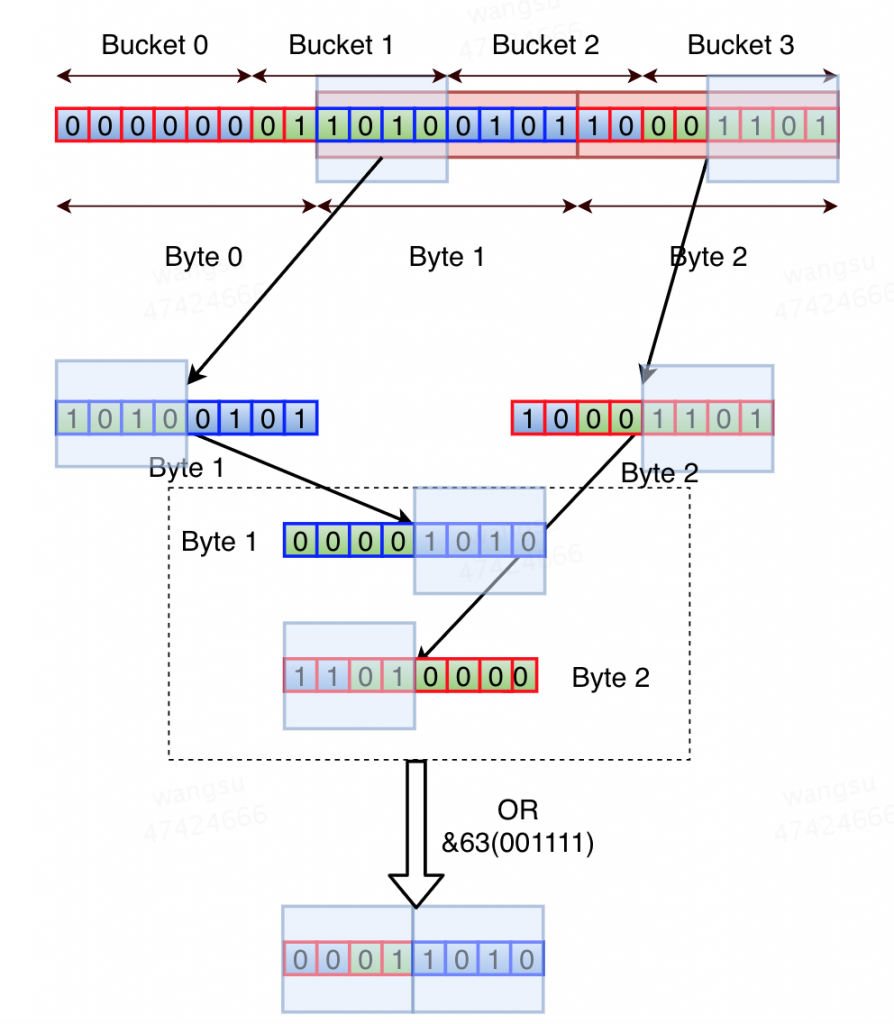
例如下图,为了获取 pos = 2 的桶的值,首先得到字节间偏移量:
bx = 6 * pos / 8 = 1
然后得到字节内偏移量:
by = 6 * pos % 8 = 4
然后将字节 b1 右移 4个比特,得到:
00001010
将 b2 左移 4个比特,得到:
1101000
按位或并且丢弃最高两位(&63)得到:
(00)011010
示意图如图所示:
将桶值设置入字符串是上述过程的逆过程,其运算过程要比从字符串中取桶值稍微复杂一点。首先还是要得到需要设置的字节间偏移量与字节内偏移量,然后进行位操作。
bx = 6 * pos / 8
by = 6 * pos % 8
例如我们要设置 pos = 7 的桶为 val = 00xx yyyy
计算出:
bx = 5,by = 4
首先操作第一个字节 b5 ,b5 字节上的桶号为 (7777 6666),将 mask (63,0011 1111) 左移 by = 4 位并取反得到新的 mask 0000 1111。将 0000 1111 与字节 5 的 (7777 6666) 按位与,得到最后的mask 0000 (6666)
将 val 左移 4位,即 val = 00xx yyyy 变成 yyyy 0000,与 0000 (6666) 按位或得到 yyyy (6666),即 val 的后 4 位被设置到了字节 5 的前 4 位(即 bucket 7 的 4 位),而字节 5 的其他比特不变。
设置第二个字节 b6 ,b6 字节上的桶号为 (8888 8877),将mask (63, 0011 1111) 右移 8 – b_y = 4 个字节,然后取反得到新的 mask 1111 1100。将 mask 与字节 6 的 (8888 8877) 按位与得到最后的mask (8888 88)00
将 val 右移 8 – 4 = 4 位得到 0000 00xx,与mask 按位或得到 (8888 88)xx,此时 val 的前 2 为被设置到字节 6 的后 2 位 (即 bucket 7 的后两位)这样就设置完成了。
获取 bucket 值的代码如下:
#define HLL_DENSE_GET_REGISTER(target,p,regnum) do { \
uint8_t *_p = (uint8_t*) p; \
unsigned long _byte = regnum*HLL_BITS/8; \ //bx 字节间偏移
unsigned long _fb = regnum*HLL_BITS&7; \ //by 字节内偏移
unsigned long _fb8 = 8 - _fb; \ //8 - by 需要 b(x+1)反向偏移的偏移量
unsigned long b0 = _p[_byte]; \ //bx 对应的字节值
unsigned long b1 = _p[_byte+1]; \ //b(x+1)对应的字节值
target = ((b0 >> _fb) | (b1 << _fb8)) & HLL_REGISTER_MAX; \ //b0 右移 _fb,b1 左移 _fb8,合并,然后取出
} while(0)
设置 bucket 值代码类似:
#define HLL_DENSE_SET_REGISTER(p,regnum,val) do { \
uint8_t *_p = (uint8_t*) p; \
unsigned long _byte = regnum*HLL_BITS/8; \
unsigned long _fb = regnum*HLL_BITS&7; \
unsigned long _fb8 = 8 - _fb; \
unsigned long _v = val; \
_p[_byte] &= ~(HLL_REGISTER_MAX << _fb); \
_p[_byte] |= _v << _fb; \
_p[_byte+1] &= ~(HLL_REGISTER_MAX >> _fb8); \
_p[_byte+1] |= _v >> _fb8; \
} while(0)
Cardin Cache
前面提到 HyperLogLog 表示的总计数值是由 16384 个桶的计数值进行调和平均后再基于因子修正公式计算得出来的。它需要遍历所有的桶进行计算才可以得到这个值,中间还涉及到很多浮点运算。这个计算量相对来说还是比较大的。
所以 Redis 使用了一个额外的字段来缓存总计数值,这个字段有 64bit,最高位如果为 1 表示该值是否已经过期,如果为 0, 那么剩下的 63bit 就是计数值。
当 HyperLogLog 中任意一个桶的计数值发生变化时,就会将计数缓存设为过期,但是不会立即触发计算。而是要等到用户显示调用 pfcount 指令时才会触发重新计算刷新缓存。缓存刷新在密集存储时需要遍历 16384 个桶的计数值进行调和平均,但是稀疏存储时没有这么大的计算量。也就是说只有当计数值比较大时才可能产生较大的计算量。另一方面如果计数值比较大,那么大部分 pfadd 操作根本不会导致桶中的计数值发生变化。
这意味着在一个极具变化的 HLL 计数器中频繁调用 pfcount 指令可能会有少许性能问题。关于这个性能方面的担忧在 Redis 作者 antirez 的博客中也提到了。不过作者做了仔细的压力的测试,发现这是无需担心的,pfcount 指令的平均时间复杂度就是 O(1)。
Calculation
有关 Redis 采用的具体 HyperLogLog 算法可以参见论文 New cardinality estimation algorithms for HyperLogLog sketches,受到篇幅所限,在这里不再赘述(大量数学推导),其代码实现如下。
uint64_t hllCount(struct hllhdr *hdr, int *invalid) {
double m = HLL_REGISTERS;
double E;
int j;
int reghisto[HLL_Q+2] = {0};
/* Compute register histogram */
if (hdr->encoding == HLL_DENSE) {
hllDenseRegHisto(hdr->registers,reghisto);
} else if (hdr->encoding == HLL_SPARSE) {
hllSparseRegHisto(hdr->registers,
sdslen((sds)hdr)-HLL_HDR_SIZE,invalid,reghisto);
} else if (hdr->encoding == HLL_RAW) {
hllRawRegHisto(hdr->registers,reghisto);
} else {
serverPanic("Unknown HyperLogLog encoding in hllCount()");
}
/* Estimate cardinality form register histogram. See:
* "New cardinality estimation algorithms for HyperLogLog sketches"
* Otmar Ertl, arXiv:1702.01284 */
double z = m * hllTau((m-reghisto[HLL_Q+1])/(double)m);
for (j = HLL_Q; j >= 1; --j) {
z += reghisto[j];
z *= 0.5;
}
z += m * hllSigma(reghisto[0]/(double)m);
E = llroundl(HLL_ALPHA_INF*m*m/z);
return (uint64_t) E;
}
主要是按照密集以及稀疏分情况调用 hllSparseRegHistro 以及 hllDenseRegHistro 获取其 Histogram,然后最后通过上一篇给出的无偏估计的公式给出估计的基数值。