HyperLogLog 算法（一）——Bitmap 与 LinearCounting

从计数谈起

在漫长的求职刷 leetcode 的过程中，会遇到一个普遍的情景，但是苦于所学的语言没有封装数据结构去描述这一情景，所以一直以来都是自己在代码里实现。直到某一天看到关于 hyperloglog 的算法，才发现本问题比想象的要复杂得多，那就是计数的问题。

所谓计数，用来统计一个集合中出现的各个不同元素的个数，由于在 leetcode 中太普遍，以至于一时间没有找到什么特别有代表性的问题可以贴在这里，但是普遍情况下使用 HashMap 实现，例如：

class Counter<T>{
   private HashMap<T, Integer> countMap;

   public Counter<T>(){
      HashMap<T, Integer> countMap = new HashMap();
   }
   public void add(T t){
      countMap.put(this.get(t) + 1);
   }

   public int get(T t){
      return countMap.getOrDefault(t, 0);
   }
}

如果计数类型是正整数，还可以考虑直接用 Index 数组计数，即数组的 Index 为计数的元素，但是前提是元素不能太大。

class Counter{
   private int[] countMap;
   
   public Counter(int maxAppearance){
      int[] countMap = new int[maxAppearance];
   }

   public void add(int e){
      if(e >= countMap.length || e < 0 || countMap[e] == Integer.MAXIMUM){
           //throw something or just return;
      }
      countMap[e] ++;
   }

   public int get(int e){
      return countMap[e];
   }
}

如果元素出现的次数不超过 2^32 – 1 次，且需要记录的是一个 int 类型的元素，那么需要 2^32 * 4B = 16 GB 的空间进行计数。如果需要记录的是一个 char 类型的元素，那么需要 2^8 * 4B = 1 KB 的空间进行记录。当然这里并没有完全利用 int 负数部分的记录能力，还可以进行一些优化使得元素最大的出现次数可以达到 2^64 – 1 次，或者有能力记录负整数部分。

在更多时候，我们只需要知道究竟有多少不同元素被统计了，这就是我们所需要说的基数计数问题(cardinality count problem)

基数计数问题

假设全集为 \(U\), 当前所有出现的元素的集合为 \(S_{i-1}\), 新到来的一个元素为 \(x_i\), 如果 \(S_{i-1}\) 中不包含 \(x_i\), 将 \(x_i\) 加入 \(S_{i-1}\), 生成 \(S_i\)。 随着统计的数据量变大，相应的储存消耗也会变大，查找 \(x_i\) 的复杂度也会提升。

基数计数拥有很多使用场景。假设某网站有 10 个关键的活动页面，网站管理者希望能知道这是个网页在一天之内被多少个独立访问者访问过，使用基数计数可以解决这一数据流实时统计系统。对于这个情景，我们可以这样设计：
i. 每一个独立访问者使用登录的会员ID+cookie标记
ii. 每一个标记作为一个基数，维护十个页面对应的十个的基数集合
iii. 每一个标记基数到来，比对基数集合中是否存在该标记，不存在则加入集合

具体而言，我们可以使用下面的方法进行实现

B 树

基数计数实现的关键点有两个，一个是快速查找对应元素，一个是快速插入对应元素。联想到数据在磁盘上的储存方式，我们可以采用 B 树的方法维护元素的集合。有关 B 树，在先前的文章中有涉及到 B+ 树相关的内容——Collection 与 HashMap， B 树可以看作是 B+ 树的简单版本， 具体的实现与性能相关可以参照 wikipedia. 在这里不再赘述。一个传统的基于 B 树的实时计算引擎大致如下图所示：

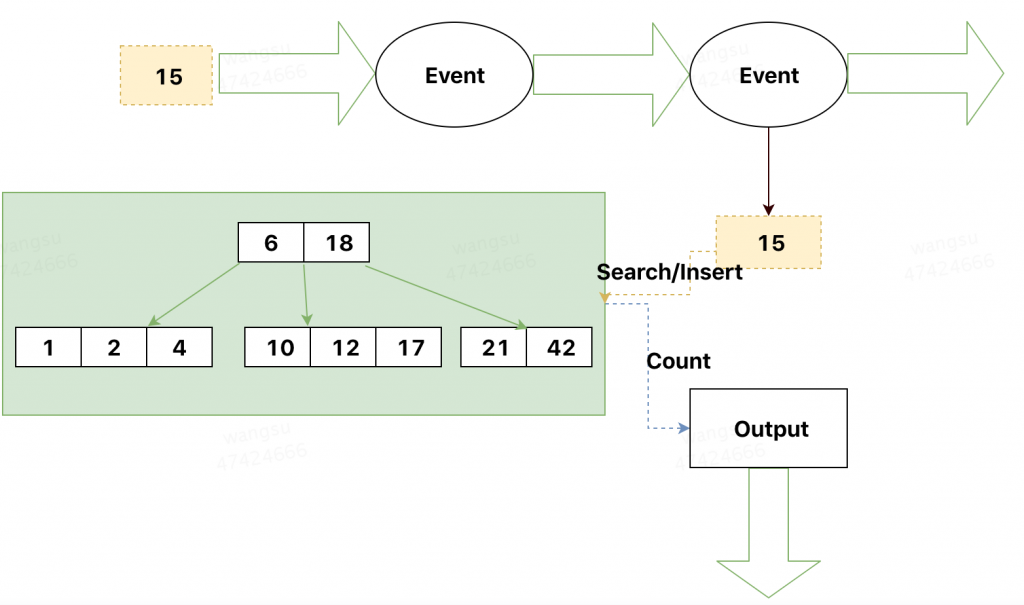
B 树实现基数计数在查找效率，插入效率以及内存上十分平衡，但是由于每一条记录都被完整保存，所以并没有任何空间上的优势。例如访问数据量巨大，不再统计 10 个页面，而是上万个链接，那么则需要在内存中维护上万个 B 树，如果一个 B 树消耗的内存是 1M，那么 10K 个B树则需要消耗 10 GB的空间， 在内存空间上这是十分巨大的消耗。

除此之外，B 树实现基数计数还有一个绕不过去的缺点在于，对于 B 树的合并几乎不可能。如果需要统计两个链接总共的 UV 数量，无法快速将两个 B 树合并为一个 B 树，除非一开始同时统计两个链接的总数量。那么 10K 个链接若干个链接合并的结果则总共需要 2^10K 个 B 树。空间使用是随着数据进行指数增长，所以在需要合并的场景下，这是不可能的。

Bitmap

为了解决 B 树无法合并的问题，可以考虑使用 Bitmap 的方式进行统计，例如上述图中的 B 树统计的结果为：
…00010000000000000000000100110000101000101011
在第 1, 2, 4, 6, 10, 12, 17, 18, 21, 42 位上 BitMap被置为了 1，和第一节记数方式中 Index 数组的记录方式类似，只是 int 数组改为了 boolean 数组。新来的数据只需要在对应位上执行或操作即可，合并只需要两个Bitmap 按位或即可。
Bitmap 最大的问题在于其长度不取决于数据的多寡，而是数据的范围（range），如果最多需要统计 10G 个数，那么需要的比特位数为 10G，即 1.25GB。即使实际统计的数只有 1 个，仍然需要 1.25 GB的空间。
所以对于 Bitmap 而言，即使合并简便，但是针对于大数据场景十分不灵活。

Linear Counting 算法

实际上，插入与查询便捷、数据合并可行，且准确的基数计算方法并不存在。但是考虑到我们往往不需要100%精准的统计数字，我们可以通过概率估计的办法，获取一个基数计数的近似值。Linear Counting 算法就是一种。
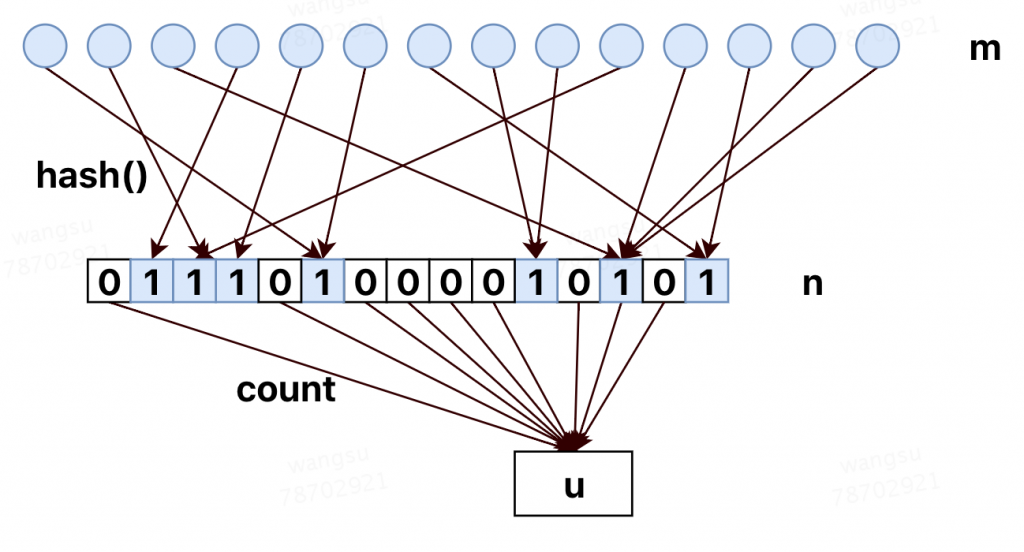
依旧考虑上一节提到的 Bitmap，如果将 Bitmap 的下标该改成每个基数对应的 Hash 值，即对于每一个基数，先进行一次哈希运算，然后将对应位置的 Bitmap 置 1。我们可以通过参数估计的方法得到总共的不重合的基数数量。具体数学描述如下：
设一哈希函数为 hash()，针对于服从均匀分布的数组 \( \overrightarrow{a}=\{ a_0, a_1, a_2, .., a_{n-1} \} \)，其哈希结果

\[ hash(\overrightarrow{a}) = \{b_0, b_1, …, b_{n-1}\}, \quad \forall 0\leq i \leq n-1, 0\leq b_i \leq m-1\]

也服从均匀分布，令 Bitmap 下标为 \( b_i\) 的位置为 \( 1\)，统计 Bitmap 中所有为 \( 0\) 的槽，记为 \( u\). 那么可以认为 \( n\) 的最大似然估计为：
\[ \hat{n}=-mlog(\dfrac{u}{m})\]
算法大致如下图所示（图中m，n标识错误，该图可理解为n个球落入m个桶中，求没有球的桶的期望）：

证明如下：
假设 “第 \( k\) 个桶在进行 \( n\) 个元素的哈希操作后值 为 \( 0\).” 这一事件为 \( A_k\), 有
\[ P(A_k) = (1-\dfrac{1}{m})^n\]
(通俗解释：n个球，每个球可能落入到第k个桶，也有可能不落入，落入的概率是1/m，不落入的概率是1- 1/m，该事件发生n次)
所以得到：
\[ E(u) = \sum_{k=1}^m P(A_k) = m(1-\dfrac{1}{m})^n \]
当 \( m, n\) 很大时，满足
\[ E(u) \approx me^{(-\frac{n}{m})}\]
所以有：
\[ n \approx -mlog(\dfrac{E(u)}{E(m)})\]
显然，由于 \( u\) 服从二项分布。
（令
\[ P(A_k) = p\]
\[ P(u=i)=C_n^i p^i (1-p)^{n-i} \]
证必）
其最大似然估计即
\[ \hat{u} = \sum_{i=0}^{n-1} \{ b_i = 0\} = u\]
（证明略）
所以 n 的最大似然估计：
\[ \hat{n}=-mlog(\dfrac{u}{m})\]
不加证明的给出，
\[ Bias(\dfrac{\hat{n}}{n})=E(\dfrac{\hat{n}}{n})-1=\dfrac{e^t-t-1}{2n}\]
\[ StdError(\dfrac{\hat{n}}{n})=\dfrac{\sqrt{m}(e^t-t-1)^{1/2}}{n}\]
\[ t=\dfrac{n}{m}\]
详细证明请参见论文“A linear-time probabilistic counting algorithm for database applications”
根据上式，我们可以推算出，如果基数的最大值为 \( N\)，允许的误差为 \( \delta\)，那么 \( m\) 应该满足:
\[ m>\dfrac{e^t-t-1}{(\epsilon t)^2} \]

在先前的文章统计模拟(二)——泊松分布与二项分布模拟中提到，当独立实验成功为 \( p\) 的二项分布的试验次数 \( n\) 很大时，可以认为二项分布近似为泊松分布，且泊松分布的方差/均值 \( \lambda=np\)。所以当 \( m, n\) 很大时，可以认为 \( u\) 服从泊松分布，且满足：

\begin{align*}&p=\lim_{m, n \rightarrow \infty}(1-\dfrac{1}{m})^n=e^{-\frac{n}{m}}\\\ &\lambda=\lim_{m, n \rightarrow \infty}mp=e^{-\frac{n}{m}}\\\ &P(u=k)=\dfrac{\lambda^k}{k!}e^{-\lambda}\end{align*}

又由于，当桶满时
\[ P(u=0)<e^{-5}=0.007\]
因此只要保证 \( u\) 的期望偏离零点 \( \sqrt{5}\)的标准差就可以保证满桶的概率不大约0.7%
所以根据允许的误差可以推算出：
\[ m>\beta(e^t-t-1)\]
其中
\[ \beta=max(5,\dfrac{1}{(\epsilon t)^2})\]
根据计算，可以得到标准差 \( \sqrt{5}\) 情况下，不同 \( \epsilon\) 以及 \( n\)的选取时，\( m\)的取值：

n	epsilon=0.01	epsilon=0.1	n	epsilon=0.01	epsilon=0.1
100	5034	80	80000	23029	10458
200	5067	106	90000	24897	11608
300	5100	129	100000	26729	12744
400	5133	151	200000	43710	23633
500	5166	172	300000	59264	33992
600	5199	192	400000	73999	44032
700	5231	212	500000	88175	53848
800	5264	231	600000	101932	63492
900	5296	249	700000	115359	72997
1000	5329	268	800000	128514	82387
2000	5647	441	900000	141441	91677
3000	5957	618	1000000	154171	100880
4000	6260	786	2000000	274328	189682
5000	6556	948	3000000	386798	274857
6000	6847	1106	4000000	494794	357829
7000	7132	1261	5000000	599692	439233
8000	7412	1412	6000000	702246	519429
9000	7688	1562	7000000	802931	598645
10000	7960	1709	8000000	902069	677040
20000	10506	3105	9000000	999894	754732
30000	12839	4417	10000000	1096582	831809
40000	15036	5680	50000000	4584297	3699768
50000	17134	6909	100000000	8571013	7061760
60000	19156	8112	120000000	10112529	8313376
70000	21117	9294

大致趋势如图所示：

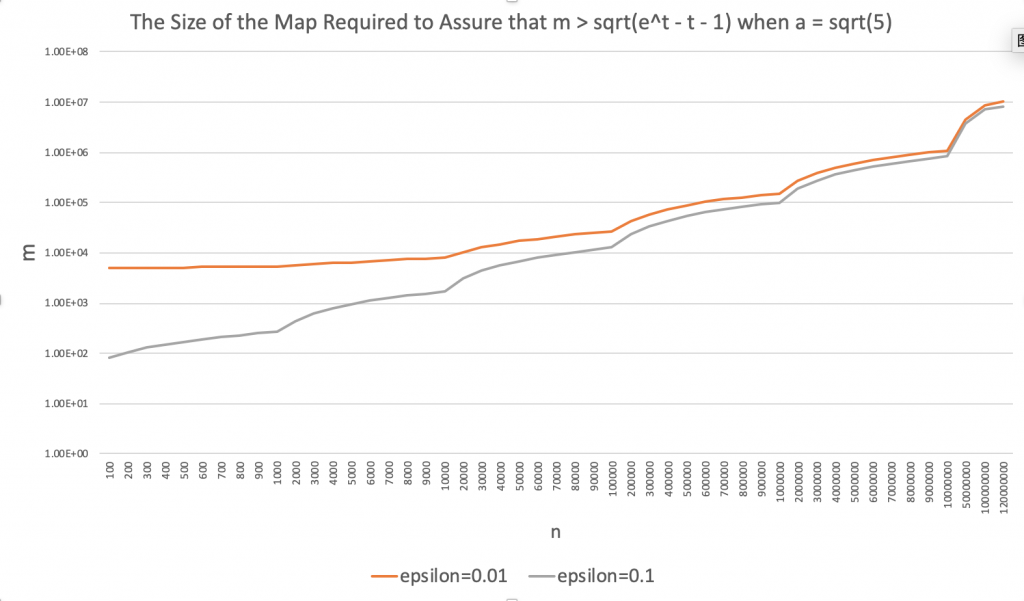
Linear Counting 算法合并直接可以按位或得到，并且按照上表可以得到，LC算法所需要的空间为传统 Bitmap 算法的 \( \frac{1}{10}\)。但是从渐进复杂性的角度看，空间复杂度仍为 O(Nmax)