在上一篇文章讨论了泛函与变分法的一些基础数学, 仅作为数学思想引出这篇文章的主要内容: EM算法.
极大似然原理
极大似然解决的问题是希望通过现有的采样数据, 解决模型已知但参数未知的问题, 也即希望通过采样的数据推测出模型的参数. 下面两个浅显的例子助于理解最大似然原理:
例1. 北京 11 月份降雨概率为 \(0.05\) , 7 月份降雨概率为 \(0.4\). 今天降雨了. 那么现在更有可能是 11 月还是 7 月?
答案是 7 月, 我们有 \(8/9\) 的概率认定现在是 7 月, 逻辑是自然的, 因为 7 月下雨的概率更大. 在上述题设中, 第一句是已知模型, 第二句是采样结果, 需要求出的即模型的具体的(离散)参数.
例2. 已知某地 16 岁男性身高符合正态分布, 现有随机普查某中学的 16 岁男性身高若干例: \({x_1, x_2, … , x_n}\) , 那么正态分布的均值与方差分别是多少?
这一例子没有例一那样容易解决, 我们假定所有的 \(n\) 个采样都是独立同分布的, 且 \(\theta\) 为模型参数, 那么上述样本的生成可以描述为:
\[f(x_1,x_2,…,x_n|\theta) = \prod_{i=1}^n{f(x_i|\theta)}\]
我们找到极大化这一项的 \(\theta\) 的值, 就可以认为该 \(\theta\) 是最有可能的参数. 由于在实际计算连乘积时经常会产生计算下溢, 所以我们一般其取对数:
\begin{align*} LL(\theta)&=log\ f(x_1,x_2,…,x_n|\theta)\\\ &=\sum_{i=1}^n{logf(x_i|\theta)} \end{align*}
此时 \(\theta\) 的极大似然估计值 \(\hat{\theta}\) 为:
\[ \hat{\theta}=arg\ max\ LL(\theta) \]
在例二中, 我们可以得到:
\[ LL(\theta)=\sum_{i=1}^n{log\ \dfrac{1}{\sigma\sqrt{2\pi}}exp(-\dfrac{(x_i-\mu)^2}{2\sigma^2})} \]
根据多元函数 \((\theta=(\mu, \sigma))\) 极值的条件:
\begin{align*} &\dfrac{\partial{LL(\theta)}}{\partial{\mu}}=0\\\ &\dfrac{\partial{LL(\theta)}}{\partial{\sigma}}=0 \end{align*}
可以得到:
\begin{align*} \hat{\mu}&=\dfrac{\sum_{i=0}^n{x_i}}{n}\\\ \hat{\sigma}&=\dfrac{\sum_{i=1}^n{(x_i-\hat{\mu})^2}}{n} \end{align*}
极大似然估计需要有以往的历史的经验对模型进行假设, 仅仅凭借猜测假设的概率分布, 很容易出现错误的结果.
在简单的贝叶斯理论相关问题中, 我们一直假设训练样本所有的属性变量都已被观测到, 即训练样本有完整性, 但是在实际中经常会无法观测到样本的所有属性. 例如上述例子中例 2, 我们观察到的数据不再是某中学 16 岁男生的身高样本, 而是全校 16 岁男生校服尺码的样本, 在这种情况下, 能否对模型参数进行估计? 这就是 EM 算法希望解决的问题.
EM 算法
假设样本为 \({x_1, x_2, … , x_n}\) , 样本中每一项存在着隐含属性 \(z\) , 我们记需最大化的变量为 \(f(x,z)\) , 其最大似然为:
\begin{align*} LL(\theta) &= \sum_i{log\ f(x_i|\theta)}\\\ &= \sum_i{log[\sum_z{f(x_i,z,\theta)}]} \end{align*}
假设对于样本每一项 \(x_i\), 隐含属性 \(z\) 符合某一分布 \(Q_i(z)\), 且满足 \(\sum_z{Q_i(z)=1}\), 那么:
\begin{align*} LL(\theta) &= \sum_i{log\ f(x_i|\theta)}\\\ &= \sum_i{log[\sum_z{f(x_i,z|\theta)}]}\\\ &= \sum_i{log\ [\sum_z{Q_i(z)\dfrac{f(x_i,z|\theta)}{Q_i(z)}}]}\\\ &\geq \sum_i{\sum_z Q_i(z)log\ \dfrac{f(x,z|\theta)}{Q_i(z)}} \end{align*}
由于 \( log(x) \) 为上凸函数, 所以根据 Jensen 不等式:
\[ E[f(x)]\geq f(E[x]) \]
注: Jensen 不等式作为表述凸性质的不等式, 有很多变形, 其最具有概括性的一种表示形式是:
假设 \(\mu\) 是集合 \(\Omega\) 的正测度,使得 \(\mu(\Omega) = 1 \). 若 \(g\) 是勒贝格可积的实值函数,而 \(\varphi\) 是在 \(g\) 的值域上定义的下凸函数,则:
\[ \varphi(\int_{\Omega} g\ d\mu)\ \leq\ \int_{\Omega}\varphi \circ g\ d\mu \]
若\(\varphi\) 是在 \(g\) 的值域上定义的上凸函数,则:
\[ \varphi(\int_{\Omega} g\ d\mu)\ \geq\ \int_{\Omega}\varphi \circ g\ d\mu \]
而概率空间即是其测度.
我们可以得到上式最后后一个不等式成立.
(进一步解释: 在上式最后一个不等式中, 测度 \(\mu\)为 \(Q_{i}(z)\), \(g\) 为从 \(z\) 到 \(\dfrac{p(x_i,z|\theta)}{Q_i(z)}\) 的映射, \(\varphi\) 为(上凸) \(log\) 函数, 所以不等式其实是:
\[ log(\int_{\Omega}\ \dfrac{p(x_i,z|\theta)}{Q_i(z)} * Q_i(z) )\geq \int_{\Omega} log(\dfrac{p(x_i,z|\theta)}{Q_i(z)})*Q_i(z) \]
的形式.)
最大似然 \(LL(\theta)\) 由 \(\theta,\ Q_i(z),\ p(x,z)\) 共同确定, 我们需要找到使 \(LL(\theta)\) 最大的一组值. 我们可以通过上述不等式不断的抬高最大似然值的下界, 对其真实值进行逼近.
EM 算法的思路是这样的:先假设 \(\theta\) 为定值, 考虑让不等式成立时的条件, 可以得到这种情况下的最大化的 \(LL(\theta)\) , Jensen 不等式等号成立的条件为: 当且仅当实值函数 \(g\) 为常数, 即
\[ \dfrac{p(x_i,z|\theta)}{Q_i(z)}=c \]
又由于 \(\sum_z{Q_i(z)=1}\), 所以 \(\sum_z{p(x_i,z|\theta)} = c\), 于是有:
\begin{align*} Q_i(z) &= \dfrac{p(x_i,z\big|\theta)}{\sum_z{p(x_i,z\big|\theta)}}\\\ &=\dfrac{p(x_i,z\big|\theta)}{p(x_i\big|\theta)}\\\ &=p(z\big|x_i,\theta) \end{align*}
这样就可以让 Jensen 不等式等号成立, 这一步我们称为E 步.
接下来我们调整 \(\theta\) , 进一步扩大 \(LL(\theta)\), 这一步为M 步.
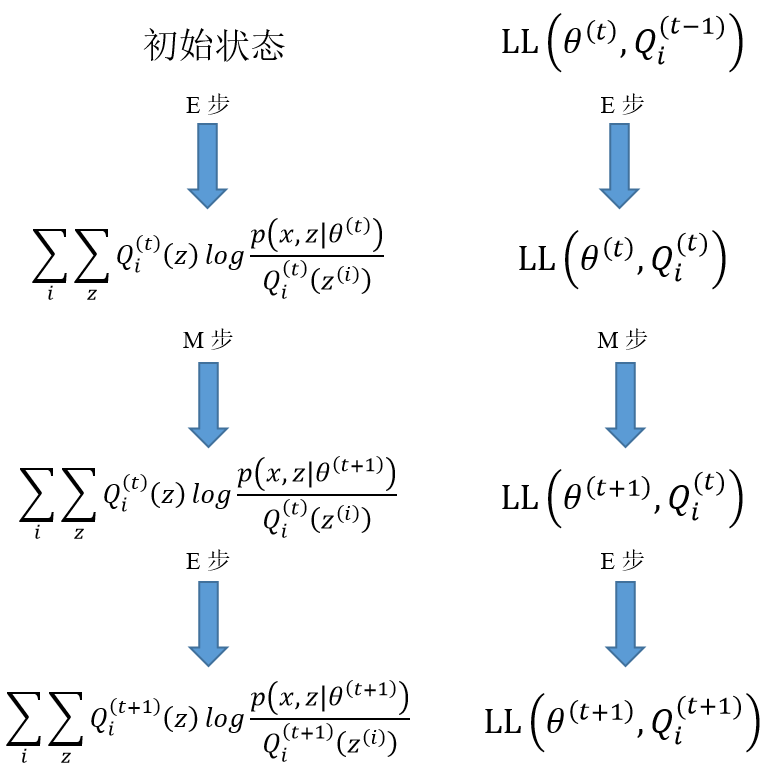
总结一下:
E 步
对于每一个 \(i\), 令
\[ Q_i^{(t)}(z) = p(z\big|x_i,\theta^{(t)}) \]
M 步
接下来令
\[ \theta^{(t+1)}=\arg\ \mathop{\max}_{\theta^{(t)}}\ \sum_i{\sum_z{Q_i(z)log\dfrac{p(x_i,z|\theta^{(t)})}{Q_i(z)}}} \]
反复迭代可以认为对最大似然的极大值进行逼近. 下图展示了逼近的方式:
EM 算法被评为数据挖掘十大经典算法之一.