本文与机器学习算法实际关联较小,仅以数学爱好作一个引子
最速曲线
一个小球沿着一个斜面下滑到某个定点, 斜面的截面是什么样的曲线时所花的时间最短? 这就是经典的最速曲线(或者称为最降曲线)的问题. 这个问题由伽利略提出, 他错误地认为答案是圆弧, 后经过牛顿和莱布尼兹等人的证明, 发现这个曲线是摆线.
谁对谁错的历史并不重要, 关键在于最速曲线的提出了一类问题, 即当未知量是一个曲线(函数), 如何求某个式子的极值? 这一类问题后来演变成了泛函分析的内容, 作为现代数学的一块基石支撑着整个现代数学金碧辉煌的大厦. 变分法作为泛函分析的最基本方法, 也被机器学习的算法所看中, 通过最优控制理论的神奇, 发挥了其很大的作用.
回到这个问题上来, 怎么去证明这个最速曲线的解是摆线的问题呢?
古典方式证明
前人通过猜测的方法, 猜测出了曲线是摆线. 有一些证明在今天看来也十分巧妙.
我们知道, 摆线是在坐标轴上滚动的一个圆, 其圆弧上以定点所形成的轨迹, 满足参数方程:
\begin{align*} \left\{\begin{matrix} x=r(\theta-sin\theta)\\\ y=r(1-cos\theta) \end{matrix}\right. \end{align*}
而著名的费马原理认为, 光的传播遵循时间最短的规则. 例如光的在折射中遵循菲涅耳定律
\[ \dfrac{v_1}{sin\theta_1} = \dfrac{v_2}{sin\theta_2} \]
其中, \(v_1, v_2\) 分别是不同介质中的光速, \(\theta_1, \theta_2\) 分别是不同介质中的入射角与折射角.
如果我们可以把光线传播的介质想象成很多层光速不同介质的叠加, 且光的速度满足小球下落的规律, 即离出发点垂直距离为 \(s\) 的介质的光速 \(v_t\) 满足 \(v_t = \sqrt{2gs}\) , 当层数足够多, 每一层足够薄, 那么其传播轨迹一定是最速曲线.
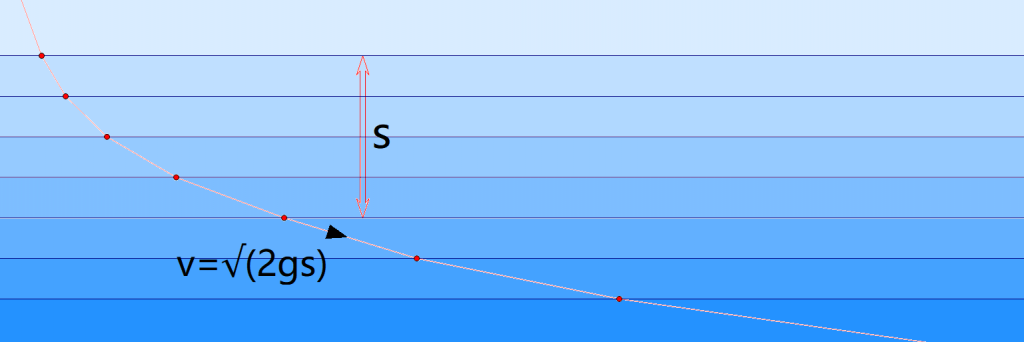
假设每一时刻的 \(v_t\) 与法线的夹角为 \(\theta_t\), 根据菲涅耳定律有:
\[ \dfrac{v_t}{sin\theta_t} = c \]
在下图中: 小球当前时刻的位置为 \(T\) , 其速度方向与摆线相切, 且在当前时刻, 点 \(T\) 当前运动轨迹的内切圆的圆心为不动点 \(A\) , 曲线的曲率半径为 \(AT\) 的长度, 由于 \(AT \perp BT\), 所以可以得到 \(AB\) 作为斜边对应圆的直径. 于是有:
\[ \angle ABT = \angle CAT = \theta_t \]
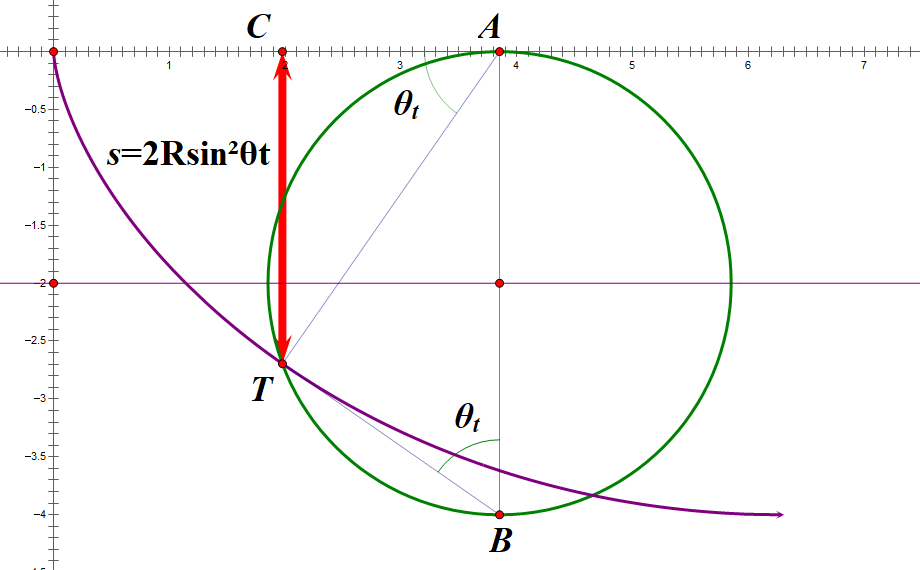
设圆的半径为 \(R\) , 可以得到:
\[ s=d[CT] = 2Rsin^{2}\theta_t\]
于是有:
\[ \dfrac{v_t}{sin\theta_t}=\dfrac{\sqrt{2gs}}{sin\theta_t}=2\sqrt{gR} \]
这样就很容易证明了摆线就是最速曲线.
变分法证明
我们将这个问题完全转化为数学语言:
设 \(C\) 为区间 \([x_0, x_1]\) 上一切满足
\begin{align*} \left\{\begin{matrix} y(x_0)=y_0\\\ y(x_1)=y_1 \end{matrix}\right.\end{align*}
的可微函数 \(y(x)\) 的集合, \(C\) 中每一个元素对应一条曲线 \(y=y(x)\), 则曲线在区间 \([x_0, x_1]\) 上的弧长 \(L\) 满足:
\[ L =\int_{x_0}^{x_1} \sqrt{1+y’^2} \,dx \]
在集合 \(C\) 中, 每一个(函数)元素都有一个数集 \(B\) 的元素与之对应, 我们把这种对应关系称作泛函. 记作:
\[ J=J[y(x)] \]
一般而言, 泛函式常用积分式表示:
\[ J=J[y(x)]=\int_{x_0}^{x_1}F(x,y,y’)\,dx \]
被积函数 \(F(x,y,y’)\) 被称为 kernel (核). (是不是想起了 SVM中 的 kernel function?)
考虑在最速曲线这一问题中, 假设起点 \(O(0,0)\), 终点 \(A(s, h)\):
\[ v=\dfrac{\,ds}{\,dt}=\dfrac{\sqrt{1+y’^2}\,dx}{dt}=\sqrt{2gy} \]
所以有:
\begin{align*} \,dt&=\sqrt{\dfrac{1+y’^2}{2gy}}\,dx\\\ t&=\int_0^{s}\sqrt{\dfrac{1+y’^2}{2gy}}\,dx \end{align*}
且满足边界条件:
\[ y(0)=0, y(s)=h \]
问题就是在所有满足条件的函数 \(y(x)\), 找出使得 \(t\) 最小的函数. 这一类泛函极值的问题也称为变分问题.
假设 \(y(x)\) 有微小变动 \(\delta y(x) \) 时
\begin{align*} J(y+\delta y)&=\int_0^{s}F(x, y+\delta y, y’ + \delta y’)\,dx\\\ &=\int_0^{s}[F(x,y,y’)+\dfrac{\partial F}{\partial y}\delta y + \dfrac{\partial F}{\partial y’}\delta y’]\,dx \end{align*}
记 \(J(y)\) 的变分:
\begin{align*} \delta J(y) &= J(y+\delta y)-J(y)\\\ &=\int_0^{s}[\dfrac{\partial F}{\partial y}\delta y + \dfrac{\partial F}{\partial y’}\delta y’]\,dx \end{align*}
在这里, 不加证明地给出: 泛函取到最值时, \(\delta J(y) = 0\) . (充要条件和一元函数类似, 为 \(0\) 的最高阶变分为的阶数为奇数, 例如, 一阶微分为 \(0\), 且二阶微分不为 \(0\), 或者三阶微分为 \(0\), 四阶微分不为 \(0\) )
不妨假设 \(y(x)\) 的变分 \(\delta y(x) = \varepsilon \varphi (x)\) , 其中 \(\varepsilon\) 为任意小的变量, \(\varphi(x)\) 为在 \([0,s]\) 上任意可微函数, 且满足 \(\varphi(0) = \varphi(s) = 0\)
根据 \(\delta J(y) = 0\) 我们可以得到:
\begin{align*} 0&=\int_0^{s}(\dfrac{\partial F}{\partial y}\varepsilon \varphi + \dfrac{\partial F}{\partial y’}\varepsilon \varphi’)\,dx\\\ &=\int_0^{s}(\dfrac{\partial F}{\partial y}\varphi + \dfrac{\partial F}{\partial y’}\varphi’)\,dx\\\ &=\int_0^{s}\dfrac{\partial F}{\partial y}\varphi \,dx + \dfrac{\partial F}{\partial y}\varphi \Bigg |_0^{s} – \int_0^s\varphi\dfrac{d}{dx}(\dfrac{\partial F}{\partial y’})\,dx\\\ &=\int_0^{s}(\dfrac{\partial F}{\partial y} – \dfrac{d}{dx}(\dfrac{\partial F}{\partial y’}))\varphi\,dx \end{align*}
由于 \(\varphi\) 具有任意性, 所以我们可以得到方程
\[ \dfrac{\partial F}{\partial y} – \dfrac{d}{dx}(\dfrac{\partial F}{\partial y’}) = 0 \]
这就是一阶的欧拉-拉格朗日方程.
我们注意到:
\begin{align*} &\dfrac{d}{dx}(F(y,y’)-y’\dfrac{\partial F}{\partial y’})\\\ =&\dfrac{\partial F}{\partial y} y’ + \dfrac{\partial F}{\partial y’}y'' – y'' \dfrac{\partial F}{\partial y’} – y’ \dfrac{d}{dx}(\dfrac{\partial F}{\partial y’})\\\ =&y'(\dfrac{\partial F}{\partial y} – \dfrac{d}{x}(\dfrac{\partial F}{\partial y’}))\\\ =&0 \end{align*}
于是我们有另一形式:
\[ F-y’\dfrac{\partial F}{\partial y’} = C \]
我们将最速曲线 \(F = \sqrt{\dfrac{1+y’^2}{2gy}}\) 带入微分方程:
\begin{align*} &\sqrt{\dfrac{1+y’2}{2gy}}-y’\dfrac{1}{\sqrt{2gy}}\dfrac{y’}{\sqrt{1+y’^2}}\\\ =& \dfrac{1}{\sqrt{2gy}}*\dfrac{1}{\sqrt{1+y’^2}}\\\ =&C \end{align*}
进行常量的替换:
\[ y(1+y’^2)=2r \]
引入参量 \(\theta\) , 并假设 \(x = X(\theta), y’ = cot\dfrac{\theta}{2}\), 可以得到:
\[ y=2rsin^{2}\dfrac{\theta}{2}=r(1-cos\theta) \]
所以有:
\begin{align*} \dfrac{dx}{d\theta}&=\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dy}{dx}}=\dfrac{rsin\theta}{cot\dfrac{\theta}{2}}=\dfrac{2rsin\dfrac{\theta}{2} cos\dfrac{\theta}{2}}{cot\dfrac{\theta}{2}}\\\ &=2rsin^{2}\dfrac{\theta}{2}=r(1-cos\theta) \end{align*}
带入边界条件可以得到:
\begin{align*} \left\{\begin{matrix} x=r(\theta-sin\theta)\\\ y=r(1-cos\theta) \end{matrix}\right. \end{align*}
变分思想
当我们需要求解一个一元或者多元函数的极值问题时, 往往是对其求微分, 从而问题转化为求解一个或者多个代数方程.
当我们需要求解一个一阶或者多阶的泛函极值问题时, 问题则转化为求解微分方程(组). 从这里可以一窥普通高等数学与泛函的相互的关联.
然而, 求解微分方程并不是一件轻松的事情, 但是我们可以通过某些迭代的方法, 把问题变得有可操作性, EM 变分算法就是其中的一种.