四种文本建模
在上一篇文章中, 从 Gamma 函数介绍到了 Dirichlet/Multinomial 共轭, 这都是为这一篇的文本建模打下基本的数学基础. 在接下来的文章中, 会介绍四种不同的文本模型. 介绍前三种的目的, 是为了引出最后想要总结的模型: LDA, 有了前三种模型的铺垫, 加上上一篇文章的数学基础, LDA 的真面目也就呼之欲出了.
Unigram Model
在这一模型中, 我们假定人写文章是这样的, 打开一本词典, 以一定概率翻到某个词, 然后写上去, 这称之为 Unigram Model, 我比较喜欢称呼为脸滚键盘模型, 也就是任何的两个词的出现都是完全独立毫无关系的. 这是最简单的词袋模型. 对应其数学模型就是: 对于一篇文档 \(d=\overrightarrow{w}=(w_1, w_2, \cdots, w_n) = \prod_{i=1}^n p(w_i) \)
假设有一个文档库 \(\mathcal{W}=(\overrightarrow{w_1}, \overrightarrow{w_2},…,\overrightarrow{w_m})\) , 可以得到, 这个文档库的分布为:
\begin{align*}p(\mathcal{W})= p(\overrightarrow{w_1})p(\overrightarrow{w_2}) \cdots p(\overrightarrow{w_m})=\prod_{k=1}^V p_k^{n_k}\end{align*}
于是我们参数估计的对象为 \(\overrightarrow{p}\) , 对这个参数进行最大似然的计算可以得到:
\[\hat{p_i} = \frac{n_i}{N} \]
\(n_i\) 为每个词 \(v_i\) 发生的频率.
Bayesian Unigram Model
这种用”频率代替概率”的最大似然算法会被贝叶斯派提出异议. 贝叶斯派会认为具体的词频的具体的概率永远不会被确定, 所以应该假定这个不确定的参数服从某一个分布, 例如狄利克雷分布.
在上一篇总结文章中给出,先验的 Dirichlet 分布加上多项分布的数据, 最后得到的后验分布依然为 Dirichlet 分布. 这种性质为我们计算提供了很大的便利.
于是在给定了参数 \(\overrightarrow{p}\) 的先验分布 \(Dir(\overrightarrow{p}|\overrightarrow{\alpha})\) 之后, 如果各个词出现的词频满足 \(\overrightarrow{n} \sim Mult(\overrightarrow{n}|\overrightarrow{p},N)\) , 那么很容易可以得到,后验分布为:
\begin{equation} p(\overrightarrow{p}|\mathcal{W},\overrightarrow{\alpha}) = Dir(\overrightarrow{p}|\overrightarrow{n}+ \overrightarrow{\alpha}) = \frac{1}{\Delta(\overrightarrow{n}+\overrightarrow{\alpha})} \prod_{k=1}^V p_k^{n_k + \alpha_k -1} d\overrightarrow{p}\end{equation}
我们根据参数的后验分布, 根据后验分布的极大值点, 对参数进行估计. 由于 \(\overrightarrow{p} \sim Dir(\overrightarrow{\alpha} + \overrightarrow{n})\) , 所以有:
\[E(\overrightarrow{p}) = \Bigl(\frac{n_1 + \alpha_1}{\sum_{i=1}^V(n_i + \alpha_i)}, \frac{n_2 + \alpha_2}{\sum_{i=1}^V(n_i + \alpha_i)}, \cdots, \frac{n_V + \alpha_V}{\sum_{i=1}^V(n_i + \alpha_i)} \Bigr) \]
于是参数 \(p_i\) 的估计为:
\begin{equation} \label{dirichlet-parameter-estimation} \hat{p_i} = \frac{n_i + \alpha_i}{\sum_{i=1}^V(n_i + \alpha_i)} \end{equation}
不加推导的给出, 整个语料的概率分布为:
\[p(\mathcal{W}|\overrightarrow{\alpha}) = \frac{\Delta(\overrightarrow{n}+\overrightarrow{\alpha})}{\Delta(\overrightarrow{\alpha})} \]
pLSA Model
简单的脸滚键盘模型来描述写文章的过程明显过于草率, 人们不可能是从字典里随机挑选词语来进行创作. pLSA 模型可以认为是比较接近正常人写文章的步骤.
人们写文章之前, 总是要先想好大体要创作的内容, 例如针砭时弊, 例如学科科普, 例如专业论文. 选定一个内容之后便会选择若干主题, 比如准备创作文章的是聚类算法的介绍内容, 那么这篇文章的主题可能有 K-means, Mixture-of-Gaussian, hierarchical clustering. 针对于每一个不同的主题, 会出现这个主题经常出现的词语. 所以 pLSA 模型认为, 一篇文章由多个主题构成, 每一个主题代表着众多词汇的一种分布.
总结一下, pLSA 认为每写一篇文章, 首先从”主题袋”中选择一个主题z, 然后从K个以主题区分的”词袋”中选择第z个词袋, 从这个词袋里挑选一个词, 重复上述过程, 完成这篇文章.
关于 pLSA 的数学模型, 由于与 LDA 的关联不是很重要, 在这里略去不表, 仅作为引子引出 LDA 模型.
LDA Model
与上面的 Unigram Model 一样, pLSA 模型会遭到贝叶斯学派的反对, 贝叶斯学派会认为决定”主题袋”的参数与K个词袋的参数不是确定的, 而是服从某一特定的分布. 和 Bayesian Unigram Model 类似, 我们选择 Dirichlet 分布作为参数的先验分布. 在 LDA 模型中, 一篇文章的过程大概是这样的:
-
从无数个以主题区分的”词袋”中选择 \(K\) 个备用;
-
从无数个”主题袋”中选择一个”主题袋”;
-
从 2 中选择的”主题袋”里抽出一个主题 z;
-
从 1 中选择的 \(K\) 个”词袋”中选择主题 z 的那个”词袋”;
-
从 4 中的词袋中抽取一个词生成.
重复 3, 4, 5 便得到一篇文章.
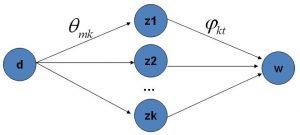
以上过程, 用概率图表示, 如下图所示:
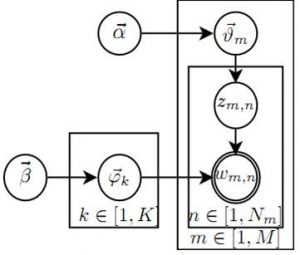
这个概率图模型大致分为两个部分:
\(\overrightarrow{\alpha} \rightarrow \overrightarrow{\theta_m} \rightarrow z_{m,n}\)表示在生成第 \(m\) 篇文档的时候, 根据”主题袋”服从的 Dirichlet 分布, 先选择了一个”主题袋” (即上述 2 过程), 然后从”主题袋”中抽选了一个主题 z (即上述3过程), 得到第 \(n\) 个词的主题 \(z_{m,n}\) . 其中, 2 过程服从 Dirichlet 分布, 3 过程服从多项分布.
\(\overrightarrow{\beta} \rightarrow \overrightarrow{\varphi_k} \rightarrow w_{m,n} | k=z_{m,n}\) 表示先从以主题区分的”词袋”中选择了 \(K\) 个 (即上述 1 过程), 从第一部分中选择的主题 z 确定”词袋”, 然后从”词袋”中抽取一个词, 得到写出的词汇 (即上述 4, 5 过程). 其中 1 过程为 \(K\) 个独立的 Dirichlet 分布, 5 过程为多项分布.
第一个部分的 \(M\) 篇文档会产生 \(M\) 个 Dirichlet-Multinomial 共轭, 第二个部分的 \(K\) 个”主题-词袋”会产生 \(K\) 个Dirichlet-Multinomial 共轭. 对于第一部分, 我们可以得到:
\[p(\overrightarrow{z}_m |\overrightarrow{\alpha}) = \frac{\Delta(\overrightarrow{n}_m+\overrightarrow{\alpha})}{\Delta(\overrightarrow{\alpha})} \]
根据先前的结论, 参数 \(\overrightarrow{\theta}\) 的后验分布:
\[Dir(\overrightarrow{\theta}_m| \overrightarrow{n}_m + \overrightarrow{\alpha})\]
由于 \(M\) 个 Dirichlet 分布相互独立, 从而我们可以得到整个语料中主题的生成概率:
\begin{align*} \label{corpus-topic-prob} p(\overrightarrow{\mathbf{z}} |\overrightarrow{\alpha}) &= \prod_{m=1}^M p(\overrightarrow{z_m} |\overrightarrow{\alpha}) \notag\\\ &= \prod_{m=1}^M \frac{\Delta(\overrightarrow{n_m}+\overrightarrow{\alpha})}{\Delta(\overrightarrow{\alpha})} \end{align*}
类似地, 我们可以得到, 整个语料库中词语的生成概率:
\begin{align*} \label{corpus-topic-likelihood} p(\overrightarrow{\mathbf{w}} |\overrightarrow{\mathbf{z}},\overrightarrow{\beta}) &= p(\overrightarrow{\mathbf{w}}’ |\overrightarrow{\mathbf{z}}’,\overrightarrow{\beta}) \notag \\\ &= \prod_{k=1}^K p(\overrightarrow{w_{(k)}} | \overrightarrow{z_{(k)}}, \overrightarrow{\beta}) \notag \\\ &= \prod_{k=1}^K \frac{\Delta(\overrightarrow{n_k}+\overrightarrow{\beta})}{\Delta(\overrightarrow{\beta})} \end{align*}
由于第一部分与第二部分相互独立, 词语与主题的联合概率密度为:
\begin{align*} p(\overrightarrow{\mathbf{w}},\overrightarrow{\mathbf{z}} |\overrightarrow{\alpha}, \overrightarrow{\beta}) &= p(\overrightarrow{\mathbf{w}} |\overrightarrow{\mathbf{z}}, \overrightarrow{\beta}) p(\overrightarrow{\mathbf{z}} |\overrightarrow{\alpha}) \notag \\\ &= \prod_{k=1}^K \frac{\Delta(\overrightarrow{n_k}+\overrightarrow{\beta})}{\Delta(\overrightarrow{\beta})} \prod_{m=1}^M \frac{\Delta(\overrightarrow{n_m}+\overrightarrow{\alpha})}{\Delta(\overrightarrow{\alpha})} \end{align*}
注意两个 production 式子中的 \(\overrightarrow{n_k}\) 与 \(\overrightarrow{n_m}\) 代表的意义不同.
MCMC
得到了概率模型的联合概率密度, 很直观地想到利用 MCMC 的方法进行采样模拟, Gibbs Sampling 作为 MCMC 的代表算法, 是一个不错的选择. 可以得到 Gibbs Sampling 中 \(z_i = k, w_i = t\) 的条件概率只和参数 \(\hat{\theta_{mk}} \cdot \hat{\varphi_{kt}}\) 正相关, 具体的推导过于复杂, 但是结论相当直观. 即: 概率分布仅仅和第一部分与第二部分的两个 Dirichlet-Multinomial 共轭相关, 结合之前 Baysian Unigram Model 中参数分布的估计值, 我么可以得到:
\begin{equation} \label{gibbs-sampling} p(z_i = k|\overrightarrow{\mathbf{z}}_{\neg i}, \overrightarrow{\mathbf{w}}) \propto \frac{n_{m,\neg i}^{(k)} + \alpha_k}{\sum_{k=1}^K (n_{m,\neg i}^{(k)} + \alpha_k)} \cdot \frac{n_{k,\neg i}^{(t)} + \beta_t}{\sum_{t=1}^V (n_{k,\neg i}^{(t)} + \beta_t)} \end{equation}
最后的 Gibbs Sampling 采样的概率图即为下图: