本文主要是对文章 LDA-math-神奇的Gamma函数 与 认识Beta/Dirichlet分布 的学习总结, 用于归纳 Gamma 函数与Beta/Dirichlet 分布的性质
从二项分布到 Gamma 函数
在高中学习概率论的时候, 第一次接触到了二项分布的概念. 二项分布问题的开始源于一个经典的问题:连续抛若干次硬币, 有多少硬币正面朝上的几率分别是多少?
这个问题是最简单的二项分布的例子. 同样的,也是从这个问题中引入排列组合中”组合”这个运算符的概念:
$$C_{n}^{k}=\frac{n!}{k!(n-k)!}=\frac{n(n-1)(n-2)…(n-k+1)}{k(k-1)(k-2)…\times 2\times 1}$$
在此的基础上, 又学习了二项展开的基本公式:
$$(a+b)^{n}=\sum_{k=0}^{n}C_{n}^{k}a^{k}b^{(n-k)}$$
后来, 又在大学阶段学习了一元函数的 Taylor 展开形式与 Maclaurin 展开形式, 也学习到了 Maclaurin 级数中, 形如 $(1+x)^{\alpha}$ 的 Maclaurin 展开式为:
\begin{split}(1+x)^{\alpha}=1+\alpha x+\frac{\alpha(\alpha-1)}{2!}x^{2}+\frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^{3}+…\\\ +\frac{\alpha(\alpha-1)(\alpha-2)…(\alpha-n+1)}{n!}x^{n}…\end{split}
此处的 \(\alpha\) 与高中接触的 \(n\) 最大的不同即 \(\alpha\) 不一定整数, 而且即使 \(\alpha\) 不是整数也并不影响 Maclaurin 级数展开的形式与计算过程. 但是如果深究细节, 便会浮现出一个问题: 由于上述的展开式的通项其实是 \(\large\frac{\alpha !}{(\alpha-k)!k!}\) 分数线上下约去相同项之后的形式. 可是新的问题出现了: \(\alpha\) 不是整数,无法进行阶乘运算。
那这就是亟待我们要解决的问题:阶乘运算在实数域的延拓是什么?
学习高等数学(数学分析)中, 在习题集里会偶尔出现下面这个函数:
\[\Gamma(x)=\int_0^{+\infty} t^{x-1} e^{-t} \,dt\]
很容易证明
\begin{align*}\Gamma(x) &=\int_0^{+\infty} t^{x-1} e^{-t} \,dt\\\ &=\int_0^{+\infty}\frac{1}{x}e^{-t} \,dt^{x}\\\ &=\frac{1}{x}e^{-t}\left.t^{x}\right|_{0}^{+\infty}+\int_0^{+\infty}\frac{1}{x}t^{x}e^{-t} \,dt\\\ &=\frac{1}{x}\int_0^{+\infty}t^{x}e^{-t} \,dt\\\ &=\frac{1}{x}\Gamma(x+1)\end{align*}
由于有 \(\Gamma(0)=\Gamma(1)=1\) , 当 \(n\) 为正整数, 具有如下性质:
\[\Gamma(n)=(n-1)!\]
所以我们可以认为 \(\Gamma(x)\) 是阶乘在实数域的延拓. 而 \((1+x)^{\alpha}\) Maclaurin展开式的形式便可化成:
\[(1+x)^{\alpha}=\sum_{k=0}^{+\infty}\frac{\Gamma(\alpha+1)}{\Gamma(k+1)\Gamma(\alpha-k+1)}x^{k}\]
关于 Gamma 函数的来源, 是一段很长的数学史, 在这里不再总结. Gamma 函数意义在于, 当对 Gamma 函数表达式本身进行归一化时, 我们会得到一个积分为 (1) 的等式:
\[\int_0^{+\infty}\frac{x^{\alpha-1} e^{-x}}{\Gamma(\alpha)} \,dx=1\]
取出积分的部分作为概率密度, 并且进行一个简单的变换 \(x=\beta*t\) , 便可得到概率论中经常使用到的 Gamma 分布:
\[\Gamma(t|\alpha,\beta)=\frac{\beta^{\alpha}t^{\alpha-1} e^{-\beta t}}{\Gamma(\alpha)}\]
其中 \(\alpha\) 称为 shape parameter, 主要决定了分布曲线的形状. \(\beta\) 称为 rate parameter 或者 inverse scale parameter, 主要决定曲线有多陡. 下图是 \(\Gamma(t|\alpha,\beta)\) 的分布图像:
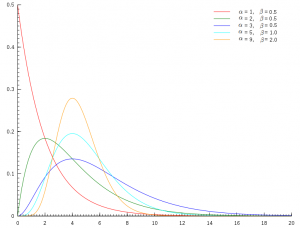
\(\Gamma(t|\alpha,\beta)\) 的分布图像
Gamma 函数到 Beta 分布
为了引入 Beta 分布,考虑如下问题
\[X_1, X_2, X_3, …, X_n \stackrel{i.i.d.}{\sim}Uniform(0,1)\]
把这 \(n\) 个统计变量从小到大排列,问第 \(k\) 个变量 \(X_{(k)}\) 的分布是什么?
在概率论中有这么个看法,几乎所有的重要的分布都可以从均匀分布中生成, 例如 Box-Muller变换, 该变换能从均匀分布变换到正态分布. (具体的证明与验证会在接下来的文章给出. ) 对于这个问题建模并不难, 我们需要考虑的概率密度函数是:
\[f_{X_{(k)}}(x)=\lim_{\Delta x \rightarrow 0} \frac{P( x \le X_{(k)} \le x+\Delta x)}{\Delta x}\]
即在均匀分布的 \([0,1]\) 的区间内, 有 \(k-1\) 个落在了 \([0,x]\) 的区间内,有 \(1\) 个落在了 \([x+\Delta x]\) 区间内, 剩下的落在了其他区间 ( 即 \([x+\Delta x, 1)]\) )内. (这里已经可以隐隐约约看出二项分布与均匀分布的关系.)
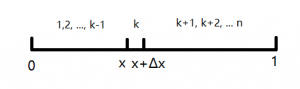
由于这 \(n\) 个变量都是独立同分布,服从均匀分布, 那么我们会得到:
\begin{align*}f_{X_{(k)}}(x) &= \lim_{\Delta x \rightarrow 0} \frac{n\times\Delta x\times C_{(n-1)}^{(k-1)}\times x^{k-1}\times(1-x-\Delta x)^{n-k}}{\Delta x}\\\ &=nC_{n-1}^{k-1}x^{k-1}(1-x)^{n-k}\\\ &=\frac{\Gamma(n+1)}{\Gamma(k) \Gamma(n-k+1)}x^{k-1}(1-x)^{n-k}\end{align*}
令 \(\alpha=k,\quad \beta=n-k-1\) ,于是我们可以得到:
\begin{equation}f(x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\end{equation}
这便得到了一般意义上的 Beta 分布.
我们接着上述的问题继续讨论, 如果又有另外 \(m\) 个随机变量 \(Y_1, Y_2, Y_3, …, Y_m \stackrel{i.i.d.}{\sim}Uniform(0,1)\). 其中有 \(m_1\) 个比 \(X_{(k)}\) 小, 有 \(m_2\) 个比 \(X_{(k)}\) 大 (\(m_1 + m_2 = m\)), 那么求现在 \(X_{(k)}\) 的分布是什么?
这里不给出具体的公式计算, 现在的问题等价于:
\[X_1, X_2, X_3, …, X_n, Y_1, Y_2, Y_3, …, Y_m \stackrel{i.i.d.}{\sim}Uniform(0,1)\]
把这 \(n+m\) 个统计变量从小到大排列,问第 \(k+m_1\)个变量 \(X_{(k+m_1)}\) 的分布是什么? 接下来的结论是显而易见的:
\[Beta(p|k,n-k+1) + Count(m_1,m_2) = Beta(p|k+m_1,n-k+1+m_2)\]
这描述的其实是体现贝叶斯思想的内容, 即先验的知识 + 观测的数据 = 后验的分布. 在本例中,观测的数据是 \(Y_i \sim B(n, p)\), 其中 \(p=X_{(k)}\), 而观测到的数据有 \(m_1/(m_1+m_2)\) 的几率落入第一个区间,\(m_2/(m_1+m_2)\) 的几率落入第二个区间. 也就是说, 当先验的知识服从 Beta 分布, 观测到的数据服从二项分布, 最终得到的后验分布依旧是 Beta 分布, 这所描述的就是 Beta-Binomial共轭 .
值得提出的是, 在 Beta 分布中, 如果 \(\alpha = \beta = 1\) , Beta分布即是在 \([0, 1]\) 之间的均匀分布. 我们对于参数的假设一般是从均匀分布开始, 如果数据都是服从二项分布, 所以在后验分布 = 参数分布 + 第一批数据 + 第二批数据 +… + 第n批数据中 对于任意的n, 最终的后验分布也一定是 Beta 分布.
同样的内容推广到高维, 即求出 \(X_{(k)}, X_{(k+1)}, …, X_{(k+l)}\)的联合分布, \(Y_i\) 中有 \(m_1\) 个比 \(X_{(k)}\) 小, \(m_2\) 个比 \(X_{(k+1)}\) 小, … , \(m_l\) 个比 \(X_{(k+l)}\) 小, 那么得到 \(X_{(k)}, X_{(k+1)}, …, X_{(k+l)}\) 的联合分布是高维的 Beta 分布, 即 Dirichlet 分布, \(Y_i\) 服从多项分布, 最后的后验的分布依然是 Dirichlet 分布. 以上贝叶斯分析过程的简单直观的表述就是:
\[Dir(\overrightarrow{p}|\overrightarrow{\alpha}) + MultCount(\overrightarrow{m})= Dir(p|\overrightarrow{\alpha}+\overrightarrow{m})\]
一般形式的 Dirichlet 分布定义为:
\begin{equation}\displaystyle Dir(\overrightarrow{p}|\overrightarrow{\alpha}) = \displaystyle \frac{\Gamma(\sum_{k=1}^K\alpha_k)} {\prod_{k=1}^K\Gamma(\alpha_k)} \prod_{k=1}^K p_k^{\alpha_k-1} \end{equation}
记 \(\Delta(\alpha)\) 为 Dir 因子:
\[\Delta(\alpha) = \frac{\Gamma(\sum_{k=1}^K\alpha_k)} {\prod_{k=1}^K\Gamma(\alpha_k)}\]
其中, 对于给定的 \(\overrightarrow{p}\) 和 \(N\) ,多项分布定义为:
\begin{equation} \displaystyle Mult(\overrightarrow{n} |\overrightarrow{p},N) = \binom{N}{\overrightarrow{n}}\prod_{k=1}^K p_k^{n_k} \end{equation}